As I develop the BGecko course Lectures on Operator Theory and Operator Algebras, it is essential to establish a rigorous overview on the hierarchy of topological spaces. In our previous essay, we defined the operator, and how they might be interpreted over both finite and infinite dimensional spaces. In Linear Algebra, we study the geometry of vector spaces and the matrices that act on them. Yet a more general framework is required to study spaces with richer or poorer structures as they undergo linear transformations in Operator Theory.

Formally, Operator Theory is (analogously) the study of Topological Spaces and the operators that act on them. For this reason, it is important to identify key features of Topological Spaces worth studying in this course. Assuming you are somewhat familiar with the definition of a topological space, lets establish a hierarchy that characterizes how these structures mathematically relate to one another (please review the diagram below):

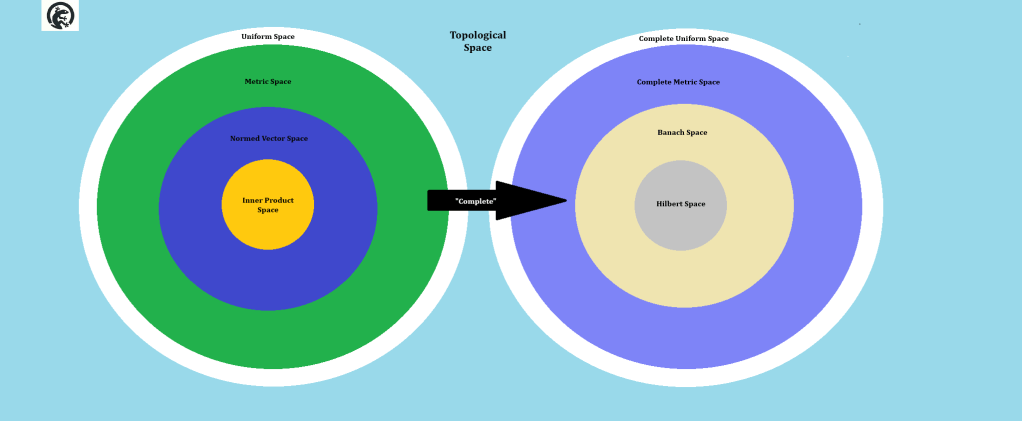
Hierarchy of Topological Spaces

In elementary linear algebra, vector spaces are typically endowed with a norm or inner product and thus are treated implicitly as metric spaces. Topology, however, introduces a broader framework of uniform spaces, which generalize the notion of metric spaces by retaining a concept of “uniform closeness” without relying on a specific distance function. Within this context, the Hausdorff completion of a uniform space arises as a natural extension of the Cauchy completion of a metric space (familiar in the study of mathematical analysis).

But completeness is not a Topological property; it should be viewed as a property that lifts the spaces on the left of the diagram, into another hierarchy that allows mathematical analysis. The right-hand side of this diagram shows their corresponding structures that are central to functional analysis and find profound applications in quantum mechanics. In this introduction, we will define each space, give examples, and clarify those properties that reveal their inherent relationship to other spaces.

Inner Product Space

The inner product space seems to be a naturally comfortable space to define before any other. In Essay I, we assumed you are already familiar with the inner product, and stated examples. However the definition should still be stated explicitly (and its properties), to show how it corresponds to other spaces in this hierarchy.

The Inner Product space is where our intuition about Euclidean angles reside. Let be any vector spaces over the field . We say is an inner product space, when it is equipped with the mapping , satisfying the following properties:

For all vectors , and ,

• Conjugate Symmetry.
  
• Positive Semi-definiteness.
  
  • if and only if .
    
• Linearity in the First Argument.
  
  • Combined with Conjugate Symmetry, this becomes Linearity in the Second Argument.
    

Notes:

To provide an example, let be a symmetric, positive-semidefinite matrix over the real numbers. Then we can define the the inner product:

Normed Vector Space

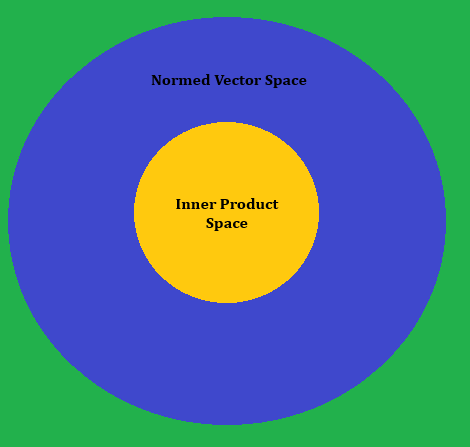
Definition:

A normed vector space is any space with a mapping , defined as the norm, satisfying the following axioms:

Axioms:

For all vectors , and ,

• Non-negativity Property. for all
  
• Positive-definiteness Property. if and only if is the zero vector.
  
• Triangle Inequality.
• Absolute Homogeneity.

Notes:

While every inner product space induces a norm that satisfies the parallelogram law, the converse is not true. A normed vector space need not satisfy the parallelogram law unless its norm arises from an inner product.

The polarization identity is an essential algebraic bridge between norms and inner products. A norm is induced by an inner product precisely when it satisfies this identity, and the existence of a polarization formula characterizes exactly those normed spaces that arise from inner product spaces.

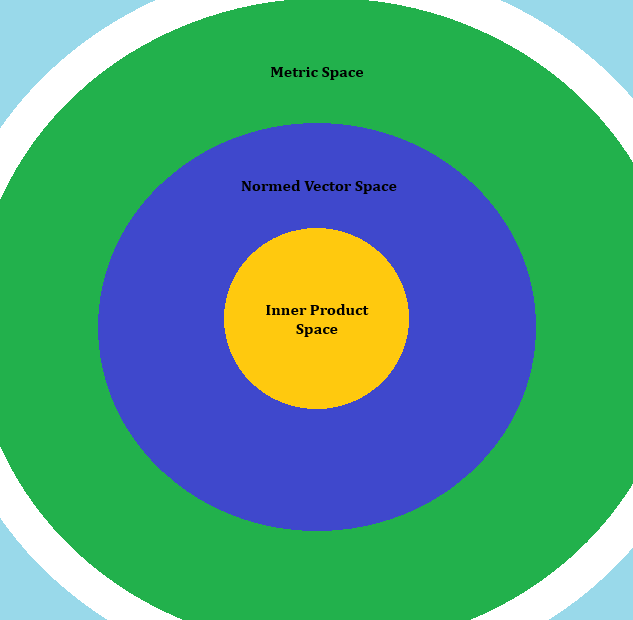
Metric Spaces