(Part One: AWGN Model)

A useful example of MAP estimation was NASA’s 1997 US patent, pertaining to the invention of a MAP decoder for digital communications. MAP decoding is a probabilistic decoding method that selects the most likely transmitted sequence given the received sequence and the channel’s statistical properties. It is fundamental in the field of communications, especially in the context of error-correcting codes. Typically a received signal can be described as follows:

where is the amplitude, is the carrier frequency, is the phase angle, and is the noise. The demodulation of phase-encoded signals can be difficult for several reasons. Even in a noise-free environment, the samples are still subjected to random perturbations as a result of difficulties with phase-encoded communication. For example, the receiver might experience an uncompensated multi-path, which is the result of the signal propagating over a multitude of paths. Another reason might be due to synchronization errors. Every device has an internal clock that may drift over time due to various reasons such as temperature fluctuations, aging, or cosmic radiation. In long-term space missions, the tiniest drift can lead to significant synchronization errors.

However, let’s first consider the simplest example of MAP decoding, i.e. decoding transmitted signals, assuming the primary source of error in a communication system is due to . This model is typically a good approximation for many practical communication channels, especially in wire-line communications.

Given a received sequence , the objective is to find — the most probable transmitted sequence of symbols out of all possible sequences — given the statistical properties of the channel. Formally the MAP estimate is given by

In the case of BPSK modulation, embodies the transmitted BPSK symbols (for ). Furthermore, is the received symbol, and is the zero-mean Gaussian noise with variance . The likelihood is given by the Gaussian

In certain systems where some sequences are more probable than others, the prior distribution can be adjusted accordingly. Assuming equal priors, the decision rule for BPSK in an AWGN channel simplifies to

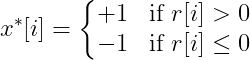
In summary, MAP decoder aims to find the most probable transmitted sequence given a received sequence, leveraging knowledge about the channel and, potentially, the statistics of the transmitted sequence. In the context of an AWGN channel with BPSK modulation, MAP decoding boils down to a simple thresholding operation on the received symbols. However, when channel coding is applied (e.g., convolutional or turbo codes), the MAP decoding process becomes more involved, often relying on algorithms like the BCJR algorithm to compute the a posteriori probabilities effectively.